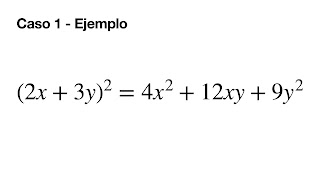Los productos notables se pueden comprender como «multiplicaciones abreviadas» de expresiones algebraicas. Los tres casos más frecuentes son:
- \( (a+b)^2 = a^2+2ab+b^2 \)
- \( (a-b)^2=a^2-2ab+b^2 \)
- \( (a+b)(a-b)=a^2 - b^2 \)
--> EJEMPLO 1 \( (a+b)^2=a^2+2ab+b^2 \)
\( (2x+3y)^2\)
Se halla inicialmente \( a^2 \), que corresponde a \( (2x)^2 \).
Luego, \( 2ab \), eso es, \( 2(2x)(3y) \).
Finalmente, el término \( b^2 \), \( (3y)^2 \).
Para terminar, se hacen las operaciones: \( (2x)^2=4x^2 \); \( 2(2x)(3y)=12xy \); \( (3y)^2=9y^2 \). Queda entonces así:
 |
| Solución al producto notable \( (a+b)^2 \) |
--> EJEMPLO 2 \( (a-b)^2=a^2-2ab+b^2 \)
\( (m-5n^2)^2 \)
El término correspondiente a \( a^2 \) es \( (m)^2 \).
Para la expresión \( 2ab \) es \( 2(m)(5n^2) \).
Y para \( b^2 \) es \( (5n^2)^2 \).
Finalmente, se hacen los cálculos: \( (m)^2 = m^2 \); \( 2(m)(5n^2) = 10mn^2 \); \( (5n^2)^2 = 25n^4 \). El resultado es:
 |
| Solución del producto notable \( (a-b)^2 \) |
--> EJEMPLO 3 \( (a+b)(a-b) = a^2-b^2 \)
\( (7p+10)(7p-10) \)
El primer término es, \( a^2 = (7p)^2 \)
Y el segundo, \( b^2 = (10)^2 \)
Por último, se realizan los cálculos de \( (7p)^2 = 49p^2 \) y \( (10)^2 = 100 \), de modo que se obtiene:
\( (7p+10)(7p-10) = 49p^2-100 \)